Aufgabe C 2
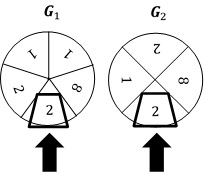Bei dem dargestellten Glücksspielautomaten sind zwei Glücksräder G1 und G2
mit fünf bzw. vier gleich großen Kreissektoren angebracht.
Bei jedem Spiel werden Sie in Drehung versetzt und laufen dann unabhängig voneinander aus.
Schließlich bleiben Sie so stehen, dass von jedem Rad genau eine Zahl im Rahmen angezeigt wird.
Der Spieleinsatz beträgt 2 €. Sind die beiden angezeigten Zahlen gleich, so wird deren
Summe in Euro ausgezahlt; andernfalls wird nichts ausgezahlt.
Der Hauptgewinn besteht also darin, dass 16 € ausgezahlt werden.
a) Ein Spieler spielt zehn Mal. Berechnen Sie die Wahrscheinlichkeit folgender Ereignisse:
A: "Das Glücksrad G1 zeigt genau fünf Mal die Zahl 1."
B: "Beim ersten Spiel beträgt die Summe der beiden angezeigten Zahlen 10."
C: "Der Spieler erhält mindestens einmal den Hauptgewinn".
(3 VP)
b) Mit einer Wahrscheinlichkeit von mehr als 95% soll in mindestens einem Spiel der Hauptgewinn erzielt werden.Berechnen Sie, wie oft man dazu mindestens spielen muss.
(2 VP)
c) Berechnen Sie, wie viel der Betreiber auf lange Sicht durchschnittlich pro Spiel verdient.(2 VP)
d) Der Betreiber möchte erreichen, dass bei zehn Spielen die Wahrscheinlichkeit für mindestens einen Hauptgewinn maximal 25 % beträgt.Dazu möchte er beim Glücksrad G2 den Mittelpunktswinkel des Kreissektors verändern, der mit der Zahl 8 beschriftet ist.
Berechnen Sie, wie weit der Mittelpunktswinkel dieses Kreissektors maximal gewählt werden darf.
(3 VP)